最良の決断をする方法（ガードナーの結婚問題より）

数年おきに盛り上がるガードナーの結婚問題（もしくは秘書問題）。

結婚問題は、1960年代にアメリカの数学者マーティン・ガードナーが記述した選択における数学的戦略です。

この戦略は、
今、交際している相手と結婚することが本当にベストの選択なのか？
今、交際している相手と結婚しなければ、将来もっといい人に出会えるかも？
あの時、交際していた相手と結婚すればよかった。
と人生の重大な決定に失敗しない方法を数学的に明らかにしたものです。

一生の伴侶を決める決断は、日常のギャンブルとはちょっと異なりますが、その選択が一生を決めるという点では人生における最大のギャンブルなのかもしれません。

◆10人のお見合い相手の中から1人を選ぶ

＜前提条件＞
① それぞれのお見合いをした直後に、その人と結婚するかどうかを決めなければいけない
② 結婚相手を決めた時点で、残りのお見合いはできない
③ 最後の相手までお見合いをしたら、その人と結婚しなければいけない

＜鉄則＞
この意思決定におけるベストな戦略は、お見合い相手全体の36.8％に達するまでは、決して結婚相手を決めてはいけない。3人目までは観察に徹し、その後、最初の3人の中で一番良かった人以上の相手に出会えたら、その人こそ最良の結婚相手となります。

＜戦略活用のコツ＞
最初の3人は、候補ではなく基準と割り切る。

＜理論の数学的説明＞
数学的な説明はかなり難解につき、ここでの説明は割愛しますが、東北大学大学院の浜田宏教授が書かれた「運命の人と出会う確率」より、シミュレーション結果のみ引用します。
横軸に見送った人数（全体人数における割合で単位は％）、縦軸に最良の相手に出会える確率をプロットしたグラフです。横軸が理論値の36.8％付近で、縦軸の最良の相手に出会える確率が最も高くなっていることがわかります。

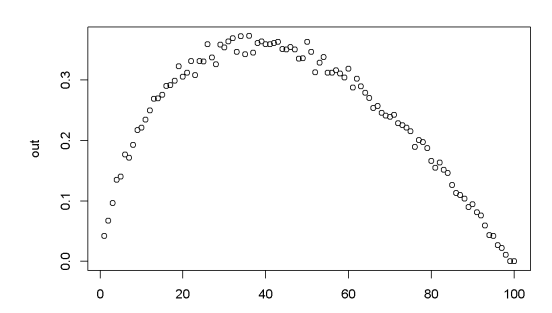
出典：東北大学大学院浜田宏教授「運命の人と出会う確率」より

＜補足＞
この戦略では、最良の結婚相手が最初の3人に含まれていた場合、ベストの相手を逸することになります。しかしながら、数学的には、これが最良の戦略となります。

◆さいごに

この戦略を活用するためには、選択できるだけの一定量の選択肢が必要です。つまり、結婚であれば自身にそれなりの魅力があってはじめて活用できる戦略となります。
ベストな選択をするためには、まずは、自身の魅力を高めないと話にならないというオチですね。