そのギャンブルには、いくら賭けるべきなのか（ケリーの公式より）

名著を読み返して、その理論をエクセルで簡単にシミュレーションするシリーズ。
今回はそのギャンブルにいくら賭けるべきなのかを教えてくれるケリーの公式（ケリー基準）です。

＜参考文献＞
天才数学者はこう賭ける―誰も語らなかった株とギャンブルの話
ウィリアム・パウンドストーン（著）、青土社、2006/11/1

例えば、手持ちの資金が100万円で、期待値70％のギャンブルがあったとします。１回の勝負に全資金の100万円を賭けてしまうと1回の負けで破産してしまいます。一方で、保守的になりすぎて１万円しか賭けなければ、勝ったとしても大勝ちは期待できません。このような時、そのギャンブルにいくら賭けるべきなのかを教えてくれるのがケリーの公式（ケリー基準）です。

 

◆ケリーの公式（ケリー基準）とは

ケリーの公式（ケリー基準）とは、複利収益率が最も高くなる最適な資金量（投資金額）を算出する公式で、投資の神様ウォーレン・バフェットや、ブラックジャックのカードカウンティングでお馴染みのエドワード・ソープが使っている手法ともいわれています。

ケリーの公式は、いろいろな形で表されますが、本稿ではギャンブラーに馴染みのあるこちらのモデルで説明します。

f*（賭けるべき資金量の割合）
＝ エッジ / オッズ
　＝ 期待値 / 見込まれる最大利益

f*：最大利益が見込まれる賭けるべき資金量の割合
エッジ：期待値：（利益×勝つ確率）＋（損失×負ける確率）
オッズ：見込まれる最大利益：※元金含まず

具体的なケースを示した方が分かりやすいので、いくつかの事例で説明します。

事例①
賭け金1ドルで、表の出る確率が50％のコイントス：
表が出たら3ドルもらえる（※元金含む）
裏が出たら１ドル失う

エッジ：
期待値＝（利益×勝つ確率）＋（損失×負ける確率）
＝(2ドル×0.5) + (ー1ドル×0.5)
＝1ー0.5=0.5

オッズ：
見込まれる最大利益：※元金含まず
3ドルー1ドル（元金）＝2ドル

f* = エッジ / オッズ
＝期待値 / 見込まれる最大利益
=0.5 / 2＝0.25=25％

つまり、毎回全資金の25％を賭け続ければ、最速で資金が増加することを示しています。

事例②
賭け金1ドルで、表の出る確率が55％のコイントス：
表が出たら2ドルもらえる（※元金含む）
裏が出たら１ドル失う

エッジ：
期待値＝（利益×勝つ確率）＋（損失×負ける確率）
＝(1ドル×0.55) + (ー1ドル×0.45)
＝0.55ー0.45＝0.1

オッズ：
見込まれる最大利益（※元金含まず）
2ドルー1ドル（元金）＝1ドル

f* = エッジ / オッズ
＝期待値 / 見込まれる最大利益
=0.1 / 1＝0.1=10％

つまり、毎回全資金の10％を賭け続ければ、最速で資金が増加することを示しています。

事例③
賭け金1ドルで、表の出る確率が60％のコイントス：
表が出たら2ドルもらえる（※元金含む）
裏が出たら１ドル失う

f* = エッジ / オッズ
=0.2 / 1＝0.2=20％

つまり、毎回全資金の20％を賭け続ければ、最速で資金が増加することを示しています。

事例④
賭け金1ドルのギャンブル：
20ドルもらえる確率　10％
5ドルもらえる確率　30％
賭け金を失う確率　60％

エッジ：
期待値＝（利益×勝つ確率）＋（損失×負ける確率）
＝(19ドル×0.1) + (4ドル×0.3) + (ー1ドル×0.6)
＝1.9＋1.2ー0.6=2.5

オッズ：
見込まれる最大利益（※元金含まず）
20ドルー1ドル（元金）＝19ドル

f* = エッジ / オッズ
＝期待値 / 見込まれる最大利益
=2.5 / 19＝0.132=13.2％

つまり、毎回全資金の13.2％を賭け続ければ、最速で資金が増加することを示しています。

 

◆簡単にエクセルでシミュレーションしてみました

＜前提条件＞
・手持ち資金は、100万円をスタートとする
・シミュレーションでは、条件ごとに100回を1セットとして、それを10セット行う
・勝率55％の場合、勝ち55回、負け45回としてシミュレーションする
・均等賭けは、毎回1万円を賭ける

＜注意＞
勝率55％のギャンブルは、100回ゲームすると55回勝つことではなく、勝率55％の抽選が毎ゲーム行われます。本シミュレーションでは、ケリー公式の効果を確認することを目的に、勝率55％のゲームでは勝ちゲーム数を55回に固定しています。

①勝率55％、均等賭け

毎回1万円を賭け続けた場合、100ゲーム後、110万円に収束します。

 

②勝率55％、ケリーの公式

f* = エッジ / オッズ
＝期待値 / 見込まれる最大利益
＝(1ドル×0.55) + (ー1ドル×0.45)
=0.1 / 1＝0.1=10％

毎回全資金の10％を賭け続けた場合、100ゲーム後、165万円に収束します。
10回すべての結果は165万円ですが、そこに至る過程には、様々なドラマが見られます。7回目のシミュレーション（水色の線）では、75ゲームの時点で462万円まで資金が増えており、あそこで止めておけばよかったと後悔するパターンです。

 

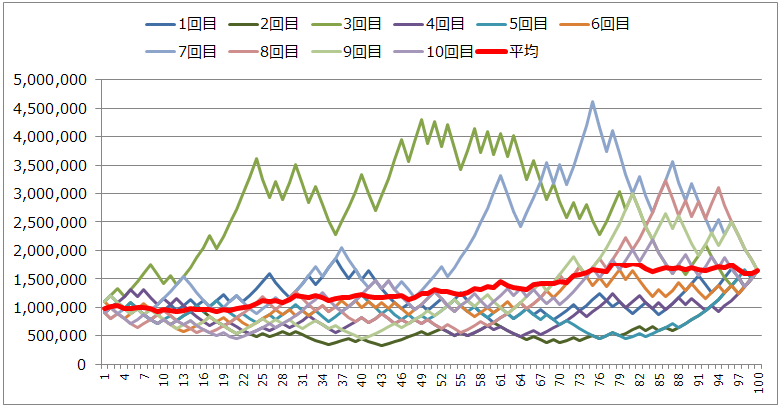
③勝率60％、均等賭け

毎回1万円を賭け続けた場合、100ゲーム後、120万円に収束します。

 

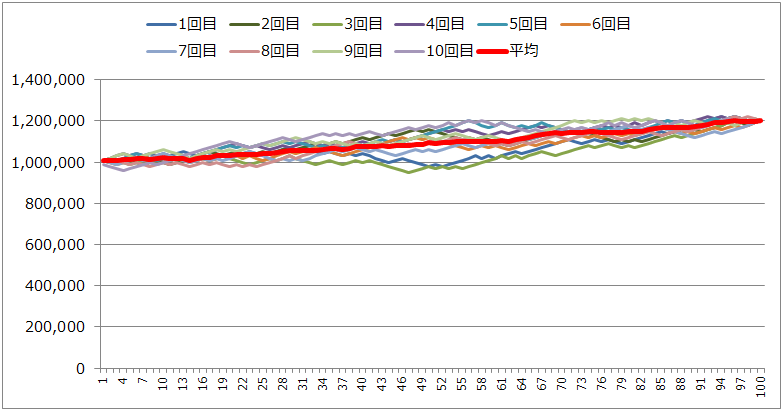
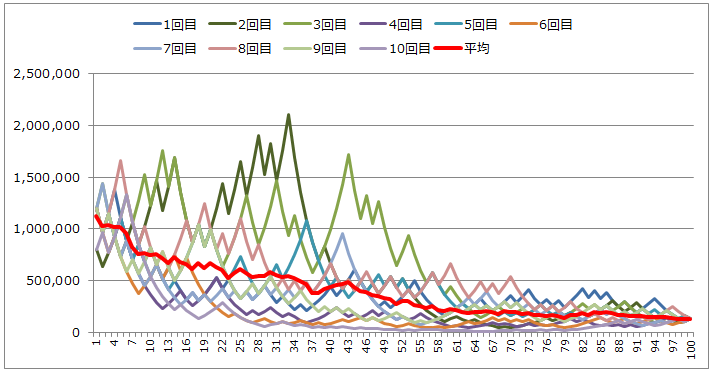
④勝率60％、ケリーの公式

f* = エッジ / オッズ
＝期待値 / 見込まれる最大利益
＝(1ドル×0.6) + (ー1ドル×0.4)
=0.2 / 1＝0.2=20％

毎回全資金の20％を賭け続けた場合、100ゲーム後、資金は大きく増加し749万円に収束します。10回すべての結果は749万円ですが、そこに至る過程には、様々なドラマが見られます。10回目のシミュレーション（薄紫の線）では、56ゲームの時点で1,839万円まで資金が増えており、あそこで止めておけばよかったと後悔するパターンです。

 

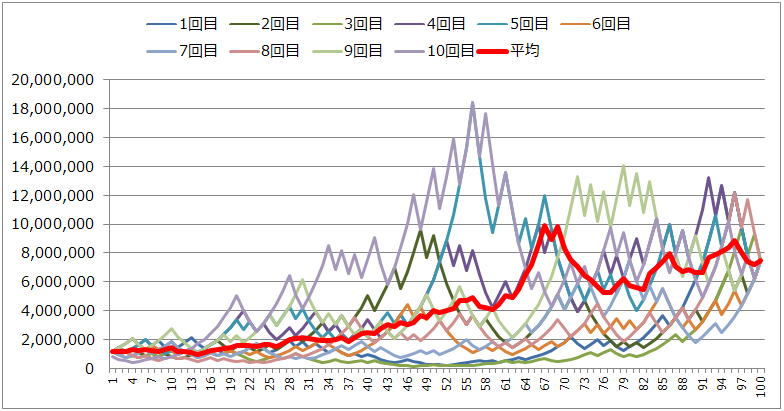
⑤勝率50％、均等掛け

毎回1万円を賭け続けた場合、100ゲーム後、100万円に収束します。

 

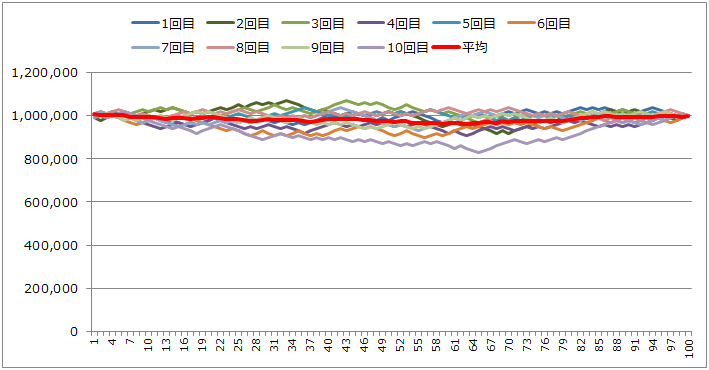
⑥勝率50％、ケリーの公式を無視

f* = エッジ / オッズ
＝期待値 / 見込まれる最大利益
＝(1ドル×0.5) + (ー1ドル×0.5)
=0 / 1＝0=0％

ケリーの公式が「0」もしくは「マイナス」を示す場合、それは賭けると損することを意味します。あえてケリーの公式を無視して、毎回全資金の20％を賭け続けた場合、100ゲーム後、資金は大きく減少し13万円に収束します。

 

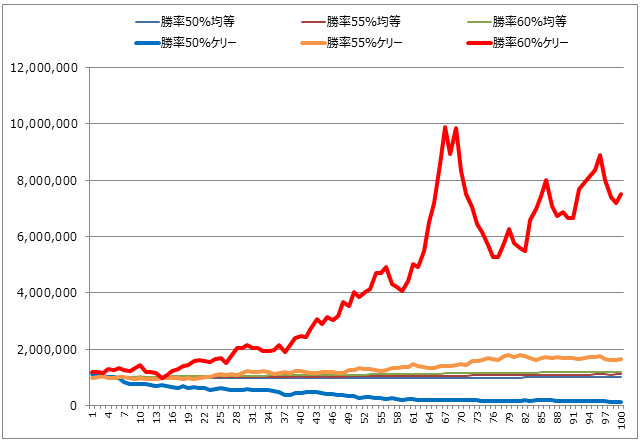
⑦総括

本シミュレーションによって、勝率と賭け方によって結果が大きく異なることがわかります。

勝率50％、均等賭け：100万円（±0万円）
勝率55％、均等賭け：110万円（＋10万円）
勝率60％、均等賭け：120万円（＋20万円）
勝率50％、ケリーの公式：13万円（▲87万円）
勝率55％、ケリーの公式：165万円（＋65万円）
勝率60％、ケリーの公式：749万円（＋649万円）

 

◆残念ながら、ケリーの公式は一般的なギャンブルには使えない

今回のシミュレーションからも明らかですが、ケリーの公式は、期待値がプラスであることを前提にしています。そのため、ハウスエッジ（胴元の取り分）が設けられ期待値がマイナスの競馬や競輪などの公営ギャンブル、カジノのテーブルゲームには利用できません。ただし、数学的に裏付けられた必勝法や確実なインサイダー情報などを持っていれば話は別です。

ちなみに、エドワード・ソープは、カードカウンティングでブラックジャックの期待値をプラスにしたことで成功したという話です。

 

◆ケリーの公式の欠点は、資金のボラティリティ（増減）が激しい

本書のデータによれば、ケリーの公式に従って賭け続けると、資金が倍になる前に半分になる確率が３分の１あり、また資金が増えた後もそこから資金が半分になってしまう可能性も50％あるとのことです。

そのため、ケリーの公式を改良して、実際のギャンブルの場では、資金の増減を抑えたハーフケリーが使われることがあります。ハーフケリーは、ケリーの公式で導いた結果が「20％」だった場合、その半分の「10％」を賭けるやり方で、リターンは4分の3に減ってしまいますが、資金が倍になる前に半分に減る確率は9分の1に抑えられるとのことです。

また、資金の増減を抑えるもうひとつ方法として、全資金が100万円あっても、全資金を50万円と仮定してケリーの公式を実践する部分ケリーもあります。

 

◆ケリーの公式まとめ

ケリーの公式が示すギャンブルの必勝法は、

①期待値がマイナスのギャンブルには賭けない
②ケリーの公式が示す値を下回る賭け金で勝負する（賭けすぎない）

つまり、期待値がプラスのゲームをいかに探すかにつきます。

 

カードカウンティングの生みの親でもある天才エドワード・ソープは、1964年頃、学術の世界から投資の世界に軸足を移し始め、以降、アービトラージ（裁定取引）で莫大な利益を上げ続けています。

裁定取引（アービトラージ）とは、同一の価値を持つ商品の一時的な価格差（歪み）が生じた際に、割高なほうを売り、割安なほうを買い、その後、両者の価格差が縮小した時点でそれぞれの反対売買を行うことで利益を獲得しようとする取引のことです。エドワード・ソープは、裁定取引の中で理論的なエッジを計算し、ケリーの公式を使って最適な資金配分を行い大成功を収めています。

 

◆さいごに

ケリーの公式が示す教訓は、ひたすら勝てる（エッジ＜分＞のある）ゲームを探して、それが見つからなければ勝負してはいけない。そして、勝てるゲームを見つけたら、賭けすぎではない範囲（ケリー基準）を守って勝負することにつきます。

一方で、ケリーの公式に従って考えると、分の悪いギャンブルはやめなさいという結論にしかならないのですが、いかに不利な状況で勝つのかがギャンブルの醍醐味だったりもします。

つまりは、分の悪いギャンブルはほどほどに。人生を破綻させるような無茶なギャンブルはしてはいけないという、至極あたりまえの答えに帰結します。