あなたなら、どれに賭ける？（ケリーの公式より）

今回は、前回の引き続きで、そのギャンブルにいくら賭けるべきなのかを教えてくれるケリーの公式（ケリー基準）です。

＜参考文献＞
天才数学者はこう賭ける―誰も語らなかった株とギャンブルの話
ウィリアム・パウンドストーン（著）、青土社、2006/11/1

例えば、手持ちの資金が100万円で、期待値70％のギャンブルがあったとします。１回の勝負に全資金の100万円を賭けてしまうと1回の負けで破産してしまいます。一方で、保守的になりすぎて１万円しか賭けなければ、勝ったとしても大勝ちは期待できません。このような時、そのギャンブルにいくら賭けるべきなのかを教えてくれるのがケリーの公式（ケリー基準）です。

ケリーの公式については、前回記事で詳しくシミュレーションしていますので、過去記事：「そのギャンブルには、いくら賭けるべきなのか（ケリーの公式より）」を参照ください。

 

◆あなたなら、どれに賭ける？

本著の中に、ケリー自身が示したとされる分かりやすい例題が紹介されています。

妻から週に1ドルずつの賭けを許されたギャンブラー。
ただし、前の週の儲けを再びつぎ込むことは妻から禁じられています。

さて、あなたがこのギャンブラーなら、下記の3つのルーレットのどれに賭けますか？

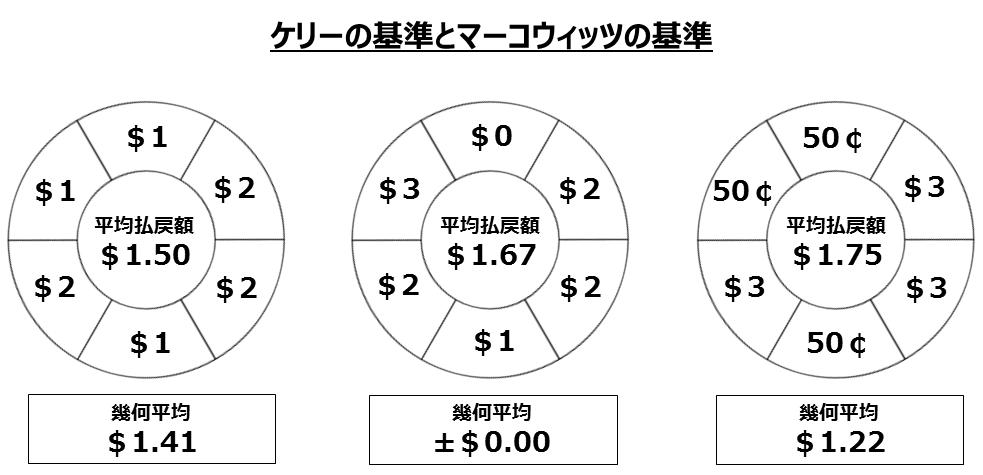
（出典：天才数学者はこう賭ける―誰も語らなかった株とギャンブルの話 P247）

平均払戻額（算術平均）：並んだ数字をすべて足し合わせて、並んだ数字の個数で割る
幾何平均：並んだ数字をすべて掛け合わせて、並んだ数字の個数でn乗根する

 

＜正解＞

左のルーレットの儲けは、52（週）×1.22（平均払戻額）＝78ドルから、元金52ドルを引いた26ドル。

真ん中のルーレットの儲けは、52（週）×1.67（平均払戻額）＝87ドルから、元金52ドルを引いた35ドル。

右のルーレットの儲けは、52（週）×1.75（平均払戻額）＝91ドルから、元金52ドルを引いた39ドル。

右（39ドル）>中（35ドル）>左（26ドル）

平均払戻額（算術平均）のもっとも大きい右のルーレットに賭けるが正解となります。この問題はほとんどの方が正解したと思います。

 

◆妻との約束をやぶって、前の週の儲けを再びつぎ込んだら？

では、次の問題です。

このギャンブラーが、妻との約束をやぶって、前の週の儲けを再びつぎ込むとしたら、どのルーレットに賭けますか？（ルーレットの出目は前問と同じです。）

 

（出典：天才数学者はこう賭ける―誰も語らなかった株とギャンブルの話 P247）

＜正解＞

ケリー基準での儲けの理論値は、

左のルーレットは、1.41^52＝67,108,864ドル
真ん中のルーレットは、0^52＝0ドル
右のルーレットは、1.22^52＝37,877ドル

これらの数字は、いずれも保証されたものではありません。運が良かったり悪かったりすれば、結果は大きく変わってきますが、左のルーレットは右のルーレットよりはるかに大きな儲けを生むことが分かります。

理論上、左のルーレットの儲けは67,108,864ドルとなり、右のルーレットの儲け37,877ドルの1,772倍の差となります。わずか0.19ポイントの幾何平均の差が1年間で約1,700倍の違いになるのは驚きです。

また、絶対に賭けてはいけないのが真ん中のルーレットです。ルーレットの目のひとつに「0」が含まれているため、常に破産の影が付きまといます。

 

◆ケリー基準まとめ

ケリーは、賭けや投資で選択しなければならないときは、結果の幾何平均が最大になるものを選べと指摘します。また、幾何平均を最大にすることは、個別の富の目標を達成する時間を最小にすることを意味します。

 

◆さいごに

ケリー基準は、賭けの利益を次回に投入してはじめて意味を持ちます。

たまにブラックジャックやバカラで延々と同額の賭け金で勝負するプレイヤーを見かけますが、大勝ちを望むなら、複利でベット金額を考えて勝負しないと駄目という話です。例えば、逆マーチンゲール法とも呼ばれるパーレー法は、勝ったら前回の賭け金を倍賭けしていくやり方。もしくは、パーレー法はハイリスク過ぎると思われる方には、勝ったら1、2、3、5、5、5…の順で賭け金を増やしていくグッドマン法などがおススメかと。

また、賭け金が固定されているパチンコ・パチスロを打つぐらいなら、勝ちが複利で狙える公営ギャンブルやカジノの方がはるかに夢があるという話ですね。